On isotropic and kinematic hardening

1. Introduction

This brief write up attempts to explain the definition of isotropic and kinematic hardening. First and foremost, in section 2, the features of inelastic response of metals are discussed, concepts of isotropic and kinematic hardening are explained in section 3.

2. Features of inelastic response of metals

Considering the results of a typical tension/compression test on an annealed, ductile, polycrystalline metal specimen (e.g. copper or Al). Assume that the test is conducted at moderate temperature (less than halfthe melting point of the solid e.g. room temperature) and at modest strains (less than 10%), at modest strain rates ( 10 to 1/100 /second).

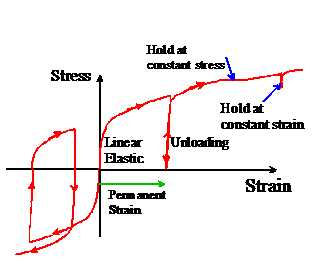
Figure 1: Features of inelastic response of metals

The results of such a test are: 

• For modest stresses (and strains) the solid responds elastically.This means the stress is proportional to the strain, and the deformation is reversible.
• If the stress exceeds a critical magnitude, the stress strain curve ceases to be linear.　 It is often difficult to identify the critical stress accurately, because the stress strain curve starts to curve rather gradually.
• If the critical stress is exceeded, the specimen is permanently changed in length on unloading.
• If the stress is removed from the specimen during a test, the stress strain curve during unloading has a slope equal to that of the elastic part of the stress strain curve.If the specimen is re-loaded, it will initially follow the same curve, until the stress approaches its maximum value during prior loading.At this point, the stress strain curve once again ceases to be linear, and the specimen is permanently deformed further.
• If the test is interrupted and the specimen is held at constant strain for a period of time, the stress will relax slowly.If the straining is resumed, the specimen will behave as though the solid were unloaded elastically.Similarly, if the specimen is subjected to a constant stress, it will generally continue to deform plastically, although the plastic strain increases very slowly.This phenomenon is known as `creep.’
• If the specimen is deformed in compression, the stressstrain curve is a mirror image of the tensile stress strain curve (of course, this is only true for modest strains.　 For large strains, geometry changes will cause differences between the tension and compression tests).
• If the specimen is first deformed in compression, then loaded in tension, it will generally start to deform plastically at a lower tensile stress than an annealed specimen.This phenomenon is known as the `Bauschinger effect.’
• Material response to cyclic loading can be extremely complex.One example is shown in the picture above in this case, the material hardens cyclically.Other materials may soften.

The detailed shape of the plastic stress strain curve depends on the rate of loading, and also on temperature.

3. Isotropic and kinematic hardening

From the behaviour discussed in section 2, one can observe that if you plastically deform a solid, then unload it, and then try to re-load it so as to induce further plastic flow, its resistance to plastic flow will have increased i.e. its yield point/elastic limit increases (meaning plastic flow begins at a higher stress than in the preceeding cycle- so we say the resistance to plastic flow increases]. This is known as 'strain hardening'.

There are different ways of modelling strain hardening for a finite element material model. Discussed below are the two simplest approaches:

• Isotropic hardening.
• Kinematic hardening.

Isotropic hardening

For isotropic hardening, if you plastically deform a solid, then unload it, then try to reload it again, you will find that its yield stress (or elastic limit) would have increased compared to what it was in the first cycle.

Again, when the solid is unloaded and reloaded, yield stress (or elastic limit) further increases. [as long as it is reloaded past its previously reached maximum stress]. This continues until a stage (or a cycle) is reached that the solid deforms elastically throughout [that is, if the cycles of load are always to the same level, then after just one cycle your specimen on subsequent cycles will just be loading and unloading along the elastic line of the stress strain curve].This is isotropic hardening.

 Essentially, isotropic hardening just means if you load something in tension past yield, when you unload it, then load it in compression, it will not yield in compression until it reaches the level past yield that you reached when loading it in tension. In other words if the yield stress in tension increases due to hardening the compression yield stress grows the same amount even though you might not have been loading the speciment in compression.

It is a type of hardening used in mathematical models for finite element analysis to describe plasticity. though it is not absolutely correct for real materials.

Kinematic hardening

Isotropic hardening is not useful in situations where components are subjected to cyclic loading.[real metals exhibit some isotropic hardening AND some kinematic hardening.

Isotropic hardening does not account for Bauschinger effect and predicts that after a few cycles, the material (solid) just hardens until it responds elastically .
To fix this, alternative laws i.e. kinematic hardening laws have been introduced. As per these hardening laws, the material softens in compression and thus can correctly model cyclic behaviour and Bauschinger effect.